Thermodynamics Review

Temperature:

The temperature of two objects “a” and “b” in thermal contact will reach thermal equilibrium eventually. This is the “0th” law of thermodynamics.

T_{a} = T_{b}

Equation of state: T,P,V,N

what is N? Avogadro number?

N $N$ is the number of particles (usually atoms or molecules) of the gas.

P = P (T, P)

P = \frac{N}{V}

Ideal Gas:

P V = N k T, P = k TP

Van Der Wahls Gas:

(P + a (\frac{N}{V})^{2}) (V - b N) = N K T

Work

$W$ is the work done on a system

= \int F_{ext} d x

is this below equation equiv to the above?

\int (- p \cdot a) d x = - \int P d V

Where $Δ x$ is an infinitesimal change in distance, and thus $Δ V = A Δ x$ where A is the area of the cylinder above.

δ W = - p d V

infinitesimal work can be given as a derivative of volume.

We can use the equation of state:

Quasi-static Process: $P = P (T, V)$ . I think

W = - \int P (T, V) d V

For an Ideal gas compressed at constant temperature:

P = \frac{N k T}{V}

If we go from some volume $V_{1}$ to some volume $V_{2}$

W = - N k T \int_{V_{1}}^{V_{2}} d V = - N k T ln \frac{V _{2}}{V _{1}}

If $\oint δ W \neq =_{0}$ , then it is not a state function

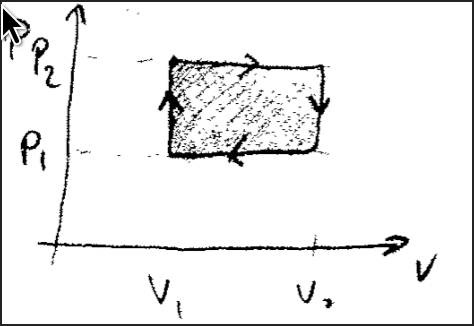
Is this the total work done? I believe so.

\oint δ W = P_{2} (V_{2} - V_{1}) - P_{1} (V_{1} - V_{2}) = - (P_{2} - P_{1}) (V_{2} - V_{1})

The first law of thermodynamics

Given a thermally isolated system: (adiabatic process)

d E = δ W

E (energy) is a state function, uniquely determined by T,P,N…

In the case of thermal contact, where $δ Q$ is not 0, this is heating/cooling.

Q is temprature? or heat? so $δ Q$ is heating/cooling?

d E = δ Q = δ W

δ E = δ Q - p d V

\oint d Q \neq = 0

(not a state function)

Equation of state for the energy

If N is constant (not adding or removing mass from the system )

E (T, V)

Ideal Gas: (mono-atomic gas)

E = \frac{3}{2} N k T

Van Der Whals gas:

E = \frac{3}{2} N k T - N (\frac{N}{V}) a

Notice how energy does not depend on volume in the ideal gas case.

Using statistical mechanics to derive this from “microcopies”

what is a microcopy

Isothermal Process for ideal gas, where T is constant

isothermal means constant temperature?

d E = δ Q + δ W = 0

δ Q = - δ W

Q_{1 \to 2} = - W_{1 \to 2} = N k T ln (\frac{V _{2}}{V _{1}})

This is the work done from a change in volume, i.e compression or expansion.

Heat Capacity and Enthalpy

Heat capacity (aka specific heat) is the amount of heating needed to change the temperature by a unit amount.

c = δ T \to 0 lim \frac{δ Q}{δ T}

For a constant volume:

δ Q = d E + p d V

and

c_{v} = \frac{δ Q}{δ T} ∣_{V} = (\frac{\partial E}{\partial T})_{V}

As an example: The monoatomic ideal gas:

c_{v} = \frac{3}{2} N k

Enthalpy

Enthalpy is thermodynamic potential? Denoted by H, where H is

H = E + p V

and

d H = d E + p d V + V d p = δ Q + V d P

You can use enthalpy to find heat capacity? For constant pressure:

(\frac{\partial H}{\partial T})_{P} = \frac{δ Q}{δ T}_{P} = c_{P}

General Relationship between Constant pressure and volume

This is constant pressure and temperature enthalpy.

H = E + p V

E (T, V)

C_{v} = (\frac{\partial E}{\partial T})_{V}

C_{p} = (\frac{\partial H}{\partial T})_{p}

C_{p} = (\frac{\partial H}{\partial T})_{P} = (\frac{\partial E}{\partial T})_{p} + p (\frac{\partial V}{\partial T})_{p}

d E = (\frac{\partial E}{\partial T})_{V} d T + (\frac{\partial E}{\partial V})_{T} d V

C_{p} = C_{v} + (\frac{\partial V}{\partial T})_{p} [(\frac{\partial E}{\partial V})_{T} + p]

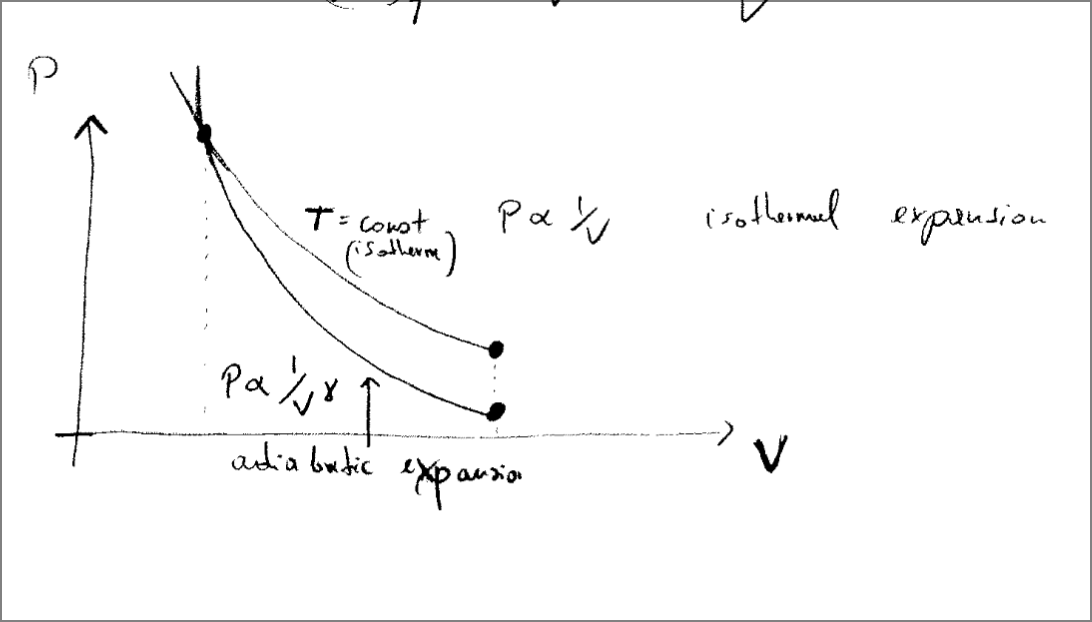
Adiabatic Processes

An adiabatic process is a process that excludes heat transfer or exchange. Perfectly insulated.

d E = δ W + δ Q

The definition of an adiabatic process:

δ Q = 0

There is no energy exchange due to temperature difference.

δ W = - P d V

This is a “quasistatic” process. Quasistatic adiabatic process.

d E = d W = - p d V

Paul's Physics Notes

Explorer

Lecture 1 Typed