Lecture 3 - Matter waves

$$\lambda =\frac{h}{p}$$

“Probably your question is not that relevant”

• Dr Persans “You should prove that” -Dr Persans “Formal.” -Dr Persans

$$\hat{A}\Psi =a\Psi$$

Set of all solutions are orthonormal

$${\delta }_{nm}=\int {\Psi }_n{\Psi }_{m}dx$$

Sin and cosine functions follow this property too

$$f(x)=\frac{1}{\pi }\left[{\int }_0^{\infty }A(k)\cos kxdk+{\int }_0^{\infty }B(k)\sin kxdk\right]$$

Where

$$A(k)={\int }_{-\infty }^{\infty }f(x)\cos kxdx$$ $$A(k)={\int }_{-\infty }^{\infty }f(x)\sin kxdx$$

This is the Fourier transform

“my question is…” -Persans

We can use Euler’s equation to rewrite the Fourier transform

“It might be” -Persans

Gaussian pulse example

We can think of a Gaussian pulse as a localized pulse, whose position we know to a certain accuracy $\Delta x=2{\sigma }_x$

Normalizing this function such that integrating over all x is 1 we get

$$f(x)=\frac{1}{{\sigma }_x\sqrt{2\pi }}{e}^{-x^2/2{\sigma }_x^2}$$

“We’re not mathematicians, we’re physicists, so we’re going to be somewhat practical about this” -Persans

$$f(x)={\int }_0^{\infty }A(k)\cos kxdx+{\int }_0^{\infty }B(k)\sin kxdx+$$ $$={\int }_0^{\infty }A(k)e^{ikx}dx+{\int }_0^{\infty }B(k)e^{-ikx}dx$$

Finding the transform

I will drop overall multiplicative constants because I am interested in the shape of $A(k)$

$$A(k)\propto {\int }_{-\infty }^{\infty }{e}^{x^2/2{\sigma }_x^2}{e}^{-ikx}dx={\int }_{-\infty }^{\infty }{e}^{-a{x}^2-ikx}dx$$ $$a=\frac{1}{2}{\sigma }_x^2$$ $$={\int }_{-\infty }^{\infty }{e}^{-(x\sqrt{a}-(ik)/2\sqrt{a}{)}^2-k^2/4a}dx$$

letting $\beta =x\sqrt{a}-\frac{ik}{2\sqrt{a}}$

$$A(k)\propto \frac{1}{\sqrt{a}}{e}^{-k^2/4a}{\int }_{-\infty }^{\infty }{e}^{-{\beta }^2}d\beta =\sqrt{\frac{\pi }{a}}{e}^{-k^2/4a}=\sqrt{\frac{\pi }{a}}{e}^{-k^2{\sigma }_x^2/2}$$

Heisenberg Uncertainty Principle

The standard deviation of k

$${\sigma }_k^2=\frac{1}{{\sigma }_x^2}$$

The result is that $\sigma_{x}\sigma_{k}=1$ for a Gaussian pulse

$k$ is the wave-number, defined as $k=\frac{2\pi }{\lambda }$. Also can be a vector to determine wave direction. The product of the wave-number width and spatial width is always equal to or greater then 1. The deBroglie hypothesis relates wavelength to momentum, deBroglie hypothesis

$$p=\frac{h}{\lambda }=\hslash k$$

Applying the deBroglie hypothesis to the above principle we get the following:

$${\sigma }_x{\sigma }_p=\frac{h}{2\pi }$$

Which is the Heisenberg Uncertainty Principle! It is frequently thought of as a measurement “problem” where you cannot know the position and momentum of a particle to an arbitrary accuracy simultaneously.

Conjugate variables

• Position and momentum are called conjugate variables and specify the trajectory of a classical particle
• If one wants to specify the position of a Gaussian wave packet, then:

$$\Delta x\Delta p=\frac{\hslash }{2}$$

• The Heisenberg uncertainty principle itself is uncertain.

Single Photon Experiments

• When single particles are sent through a system, there is interference even though there is no way for interference to occur with single particles.
• The wave function takes all possible paths at once, which is cool and weird. The wave function interferes with itself, which allows an interference pattern to form.
• If a measurement of which path the particle takes is done, the interference pattern is destroyed.
• Leads to many-worlds hypothesis. Quack science but interesting to look into. See the book timeline

Normalized Probability

$$P_{density}dx={\Psi }^{\ast }\Psi dx$$

• Given the probabilities for a set of outcomes, we can find useful quantities, like the average* (or expectation value) of a result q
• Variance = Dispersion average=mean=expectation value

Continuous Distributions

Finding expectation value Normalize first!!!

$$⟨x⟩={\int }_0^{\infty }xP(x)dx$$ $$⟨q(x)⟩={\int }_{-\infty }^{\infty }q(x)P(x)dx$$

Superposition

If you have two functions ${\psi }_1$ and ${\psi }_2$, two physically realizable states of a system, then the linear combination $\psi =c_1{\psi }_1+c_2{\psi }_2$ is also a possible state.

Normalization

Sometimes you have to normalize functions yourself that lead to an integrated probability that is not already 1. MAKE SURE YOUR FUNCTIONS ARE NORMALIZED

Schrodinger equation

There are relativistic forms of this equation. See Dirac Equation. Exists in 1d, 3d, time dependent, and time independent flavors. Time independent also known as energy eigenvalue equation.

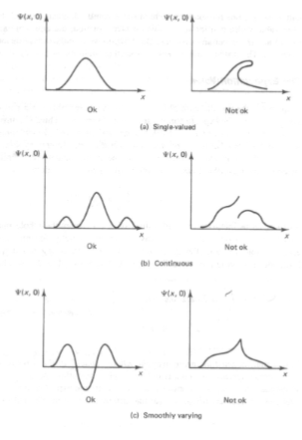
Physical Constraints on wave functions

• has to be normalizable (gotta exist somewhere)
• has to be single-valued (cant have two probabilities at same point )
• has to be continuous (or you’ll have infinite energy)
  • no kinks!

Examples of Wave functions

Expectation values

• Operators, quantum mechanics, etc etc etc