Bullet Points
- Cartesian vs Spherical cords
- Examples used are 3D box, H-atom
- Angular momentum
Angular momentum on z axis
$\hat{L}_{z}$ and $\hat{L}_{y}$ commute, but $\hat{L}_{x}$ and $\hat{L}_{y}$ do not
Bound States and Free particle
- Similar to 2-d problems, there are “free” states and “bound”’ states.
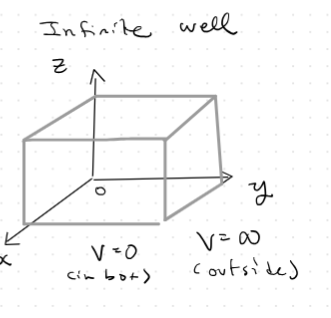
- We can use separation of variables in Cartesian/spherical coordinate systems.
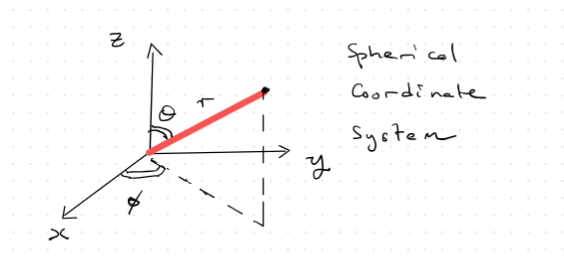
- Potential can be modeled by the following: $$ V(r) \propto -\frac{1}{r} \propto \frac{1}{\sqrt{ x^{2}+y^{2}+z^{2} }}
-\frac{\hbar^{2}}{2m} \left[ \frac{d^{2}\psi}{dx^{2}}+\frac{d^{2}\psi}{dy^{2}} +\frac{d^{2}\psi}{dz^{2}} \right]= E\psi(x,y,z)
\Psi(x,y,z) = \phi_{x}(x) \phi_{y}(y)\phi_{z}(z)