2024-01-17

Quantum Simulation

• Use to study small physics models quantum mechanically

Ex. Ising Model

• If you can get the Hamiltonian, you can solve the system with a quantum computer

$$H_{ising}=-J\sum _i{\sigma }_1^z\dots$$

Problem: Noise in system Answer: Noise mitigation techniques (eg. Zero-Noise Extrapolation ) Very physics-y approach to quantum computing. More classical approach

Quantum Error Prevention

• Big problem with quantum computers is noise

• A single photon can disrupt whole system by propagating down the system

• See N&C Chapter 10

  • Also need to review chapters 1&2

• Come up with ways to remove noise from the ground up vs removing noise from the final product Idea: Quantum information from local noise by encoding non-locally in multiqubit states Local noise: Photons, etc Why? We need very low error rates for quantum computing. Classical computers have $\sim 1$ in $10^{17}$ error rate. Quantum computing is very powerful but very fragile.

• Perfect accuracy isn’t needed, especially for systems that cannot be classically computed.

• Quantum computing errors are harder to fix, because errors are persistent and continuous. Where did quantum error correction/prevention start?

• Peter Shor 96’: Fault tolerant quantum computing

• Alexander Kitaev 97’: Topological codes in 2D

• Gottesman 97’: Stabilizer codes We want to eventually get to Gottemans research in stabilizer codes.

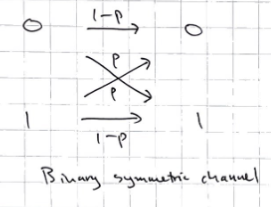
The Classical Repetition code

• Takes a classical bit, with probability p that it gets flipped to a 1 or to a 0. p probability of error .
• 1-p probability of not error.
• This is known as a binary symmetric channel
• Can protect against these flips with 3-bit repetition code
  • Encode:
    • $0\to \bar{0}=000$
    • $1\to \bar{1}\to 111$
      • Cloning?
    • $\bar{1}$ and $\bar{0}$ are logical 1s and 0s
    • Noise correction
      • $\bar{0}=000\to 100$
      • Corrects to $000$ via majority voting
    • Probability of 2,3 flips
      • These are only discrete errors
    • Probability of 2 or 3 flips

$$p_e=\left(\begin{array}{c}3\\ 2\end{array}\right)p^2(1-p)+p^3=3p^2-2p^3$$

You can graph this error percentage

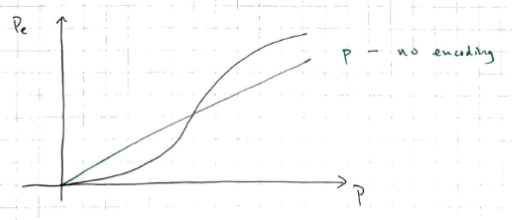
• Key points
  • Dealing with classical bits
  • Repeat the bit and use majority vote to calculate probability and correct bit
  • You can use an $n^{th}$ number of repeating bits
  • Maximize $p$ and determine what level of error is acceptable

EXERCISE! (do at home) Calculate for case of 5 bit repetition probability of error ($p_e$) for having 3,4,5 bit flips.

This also happens to be a binomial distribution

The 3-Qubit bit flip code

• Combining this and phase flip code give Shor code
• Quantum!
• Might worry about:
  • No cloning theorem
    • Can’t do classical repetition code, because cloning the information breaks it
    • $|\psi ⟩!\to |\psi ⟩|\psi ⟩|\psi ⟩$
    • $|\psi ⟩=a|0⟩+b|1⟩$
      • normalized:
      • $|\psi ⟩=\frac{|0⟩+|1⟩}{\sqrt{2}}$
      • Bell state:
      • $|\psi ⟩=\frac{|01⟩\pm |10⟩}{\sqrt{2}}$
      • The two states (1 and 0) are entangled, when you make a measurement of an observable ($\mathcal{O}$) you use an operator on the wave function
      • $⟨\psi |\mathcal{O}|\psi ⟩=⟨\mathcal{O}⟩$
  • Errors are continuous (not discrete)
  • Measurement destroys quantum information (QI)
• All these things are not a problem!

The 3 Qubit bit flip code can correct a single flip.

$$|1⟩\to |\bar{0}⟩=|000⟩$$ $$|1⟩\to |\bar{1}⟩=|111⟩$$

The general quantum state is given by a a superposition of 0 and 1

$$a|0⟩+b|1⟩\to a|000⟩+b|111⟩\equiv a|\bar{0}⟩+b|\bar{1}⟩$$

Encoding circuit: 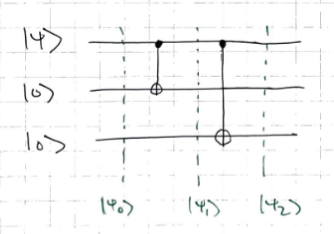When extra qubits are introduced, they’re known as ancillas.

$$|{\psi }_0⟩=|\psi ⟩|0⟩|0⟩=(a|0⟩+b|1⟩)|0⟩|0⟩$$ $$|{\psi }_1⟩=(a|00⟩+b|11⟩)|0⟩$$ $$|{\psi }_2⟩=(1|000⟩+b|111⟩)$$

What does this protect against?

$$a|0⟩+b|1⟩\to a|000⟩+b|111⟩$$

A bit is flipped (Pauli x operator)

$$a|100⟩+b|011⟩$$

Naive measurement

$$|100⟩w.p|a{|}^2$$ $$|011⟩w.p|b{|}^2$$

Cant measure directly, will collapse wave function Need subtlety!

2-step error correction

• First step- Detect which bit is flipped
  • Error detection (syndrome measurement)
• Second step- Recovery
  • Getting back what you had
• Observables
• apply $z_1$ and $z_2$ to first and second bit respectively

$$z_1=\left(\begin{array}{cc}1& 0\\ 0& -1\end{array}\right)$$

• If there was a bit flip on any one of the 3 bits, a specific state is returned that mirrors the state of the system. You can use this to detect which bit is flipped and recover the system EXERCISE! Check to see if applying matrices works

This way you’re not accessing a or b, bypassing the wave function collapse that would otherwise occur.

• Any error that works, this can fix
• Only works for single bit flips though

Look into tensor products $\otimes$

3 Qubit phase flip code

• A phase error/flip is a when the bits have not been flipped, but the phase (polarity?) has been flipped

$$\frac{|000⟩+|111⟩}{\sqrt{2}}\to \frac{|000⟩-|111⟩}{\sqrt{2}}$$

• After discussion:
  • $|\bar{0}⟩=|+++⟩$
  • $|\bar{1}⟩=|111⟩$
  • Doing same thing as before but with different basis
  • $|\pm ⟩=\frac{|0⟩\pm |1⟩}{\sqrt{2}}$
• Encoding circuit:
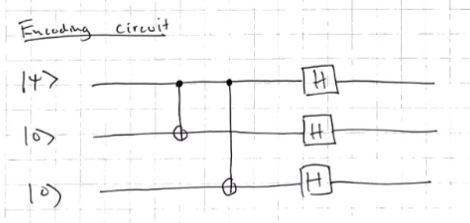
• Use Hadamard gate (H) ( why only hadamard gates on ancillias on board?)
  • Turns 0 and 1 into + and -
  • At the point before the Hadamard gate similar to 3-qubit bit flip code
• Phase flip

$$|\pm ⟩=\frac{1}{\sqrt{2}}(|0⟩\pm |1⟩)\to \frac{1}{\sqrt{2}}(|0⟩\mp |1⟩)=\mp$$

${\psi }_1$ is after the noise.

Put bit flip and phase flip together to make Shor code, very powerful! can correct any error on single qubit