Paul Lea Homework 1

1. The photoelectrons ejected in the photoelectric effect seem to appear instantaneously. In particular, no time delay has been observed, even with light of very low intensity. In classical physics. the energy of the electromagnetic wave is spread out uniformly over the surface of the metal. In this picture. calculate the amount of time it would require for 1 eV of energy (a typical binding energy) to be absorbed by an atom in a metal located 1 m away from a 1-watt bulb. Take the area of the atom to be $10^{-20}{m}^2$ . Suggestion: What fraction of the incident flux is absorbed by the atom

$$r=1m$$

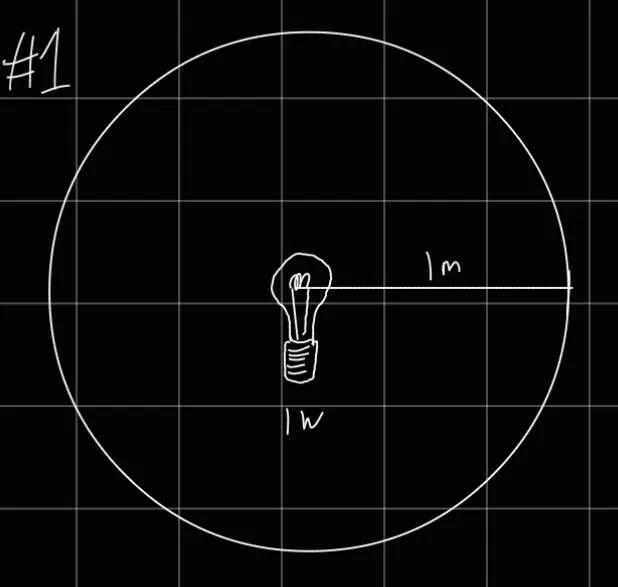
Surface Area of sphere

$$A_{sphere}=4\pi r^2=4\pi m^2$$

Ratio of areas

$$\frac{A_{atom}}{A_{sphere}}\approx 7.95775E-21$$

Calculating flux

$${\Phi }_E=7.9577E-21\frac{W}{m^2}=\frac{J}{s\cdot m^2}$$

\Phi_{E } = 0.049672274 \ \frac{ev}{s \cdot m^{2}}

\frac{1ev}{\Phi_{E}} = 20.132 \text{ seconds}

$$2.\ast \ast Townsend\mathrm{1.13.}Themaximumkineticenergyforelectronsejectedfromsodiumis1.85eVforradiationof300nmand0.82eVforradiationofwavelength400nm.UsethisdatatodeterminePlanck’sconstantandtheworkfunctionofsodium.\ast \ast$$

K=h\nu-W

1.85ev = \frac{hc}{300nm} - w

0.82ev = \frac{hc}{400nm} - w

1.85ev - \frac{hc}{300nm} =- w = 0.82ev-\frac{hc}{400nm}

1.85ev - \frac{hc}{300nm} = 0.82ev-\frac{hc}{400nm}

1.03ev - \frac{hc}{300nm} = -\frac{hc}{400nm}

1.03ev = h\left( \frac{c}{300nm}-\frac{c}{400nm} \right)

\frac{1.03ev}{\left( \frac{c}{300nm}-\frac{c}{400nm} \right)} = h

\frac{1.03ev}{1000000000000000 - 750000000000000} =h

\frac{1.65024E-19 \ J}{1000000000000000 - 750000000000000} =h

```mathpad %$1:=103/100 %$2:=103/100 %$3:=1000000000000000 %$4:=1000000000000000 %$5:=1000000000000000 %$6:=750000000000000 %$7:=250000000000000 1.65024E-19/250000000000000=~? ``` Planck's Constant $\approx 6.60096E-34$. Approximates literature values. Finding work function of sodium:

1.85ev = \frac{hc}{300nm} - w

$$Solveforw$$

1.85ev - \frac{hc}{300nm} =- w

$$‘‘‘mathpadh:=6626/10000000000000000000000000000000000000c:=300000000(h\ast c)/300E-9=?‘‘‘$$

1.85ev - 6.626e-19 J = 1.85ev - 4.1356241ev =-2.2856241 = -w

$$workfunctionofsodiumis$$

2.2856241ev

$$3.\ast \ast Townsend\mathrm{1.15.}SupposeaphotonwithawavelengthequaltotheComptonwavelengthmakesacollisionwithafreeelectroninitiallyatrest.Whatistheenergyofthefinalphotonifitisbackscatteredat180degrees?Howmuchkineticenergyistransferredtotheelectron?\ast \ast InitialEnergy$$

E=\frac{hc}{\lambda} = mc^{2} = 0.511\ MeV

$$Wavelengthofscatteredphoton$$

\lambda’ - \lambda = \frac{h}{mc}(1-\cos 180)

\lambda’ - \lambda = \frac{2h}{mc}

\lambda’ = \frac{2h}{mc}+ \lambda =\frac{3h}{mc}

$$Energyofscatteredphoton$$

E’ = \frac{hc}{\lambda’} = \frac{(mc)hc}{3h} = \frac{1}{3}mc^{2} =0.1707\ MeV

$$Andtheelectrongainskineticenergygivenby$$

K=E-E’=\frac{2}{3}mc^{2}= 0.3403\ MeV

4. **Townsend 1.18. (a) Suppose that the probability amplitude for a photon to arrive at a detector is $1/ (1+i)$. What is the probability that the detector records a photon? (b) What is the probability of· detecting a photon if the probability amplitude equals i? (c) Determine the probability of detecting a photon if the probability amplitude is**

\frac{1}{1+i} +i

$$\ast \ast d)Showthat\ast \ast$$

\frac{1}{1+i}-i

$$\ast \ast isnotavalidprobabilityamplitude.\ast \ast \ast \ast Suggestion:Whatwouldbetheprobabilityofdetectingaphotonforthisamplitude?\ast \ast \ast \ast a.\ast \ast Probabilityofaneventisgivenby$$

z^{*}z

$$so$$

\frac{1}{1-i} \frac{1}{1+i}

$$givestheprobabilityofdetection.Simplified,thatyields:$$

\frac{1}{2}

**b.** If the probability amplitude is equal to $i$, the probability of detection is given by

-i(i) = 1

$$soitis1,ora100\ast \ast c\ast \ast .Givenprobabilityamplitude$$

\frac{1}{1+i} +i

$$Detectionprobabilityis$$

(\frac{1}{1-i} -i)\frac{1}{1+i} +i

$$Multiplyingbothtermsbytherespectivecomplexconjugate$$

\left( \frac{1-i}{2} \right)\frac{1+i}{2}

$$andthismultipliedoutisequalto$$

\frac{1}{2}

$$Whichisthedetectionprobabilityd.Thisisnotavalidprobabilityamplitude,thiscanbeprovenbytryingtocalculatethedetectionprobability$$

(\frac{1}{1-i}+i)\frac{1}{1+i}-i

(\frac{1}{2}(1 + 3i))(\frac{1}{2}(1 - 3i))

\frac{5}{2}

You don't need to be Einstein to realize why a $>1$ probability doesn't make sense 5. **Townsend 1.20. Rewrite each of the following complex numbers in each of the forms $z=x+iy$ and $re^{i\phi}$, where 𝑥, 𝑦, 𝑟, 𝑎𝑛𝑑 𝜙 are real numbers. State logic and/or show work.** a. $(1+2i)^{2}$

(1+2i)(1+2i)=1 + 4i +4i^{2}

$z=x+iy$ form:

z=-3+4i

r=\sqrt{ (-3)^{2}+4^{2} } = 5

\phi = \arctan\left( -\frac{4}{3} \right) \approx 0.927

$re^{i\phi}$ form:

5e^{-i0.927}

b. $\frac{1}{1+i}$

\frac{1}{1+i} \frac{1-i}{1-i}

=\frac{1}{2} + \frac{1}{2}i

$z=x+iy$ form:

z=\frac{1}{2} + \frac{1}{2}i

r=\sqrt{ \left( \frac{1}{2} \right)^{2}+\left( \frac{1}{2} \right)^{2} } = \sqrt{ \frac{1}{2} } \approx 0.7071

\phi = \arctan\left( \frac{\frac{1}{2}}{\frac{1}{2}} \right) = \frac{\pi}{4} \approx 0.7854

$re^{i\phi}$ form:

\sqrt{ \frac{1}{2} }e^{i\pi/4} \approx 0.7071e^{i 0.7854}

c. $\sqrt{ 3-4i }$ Complete the square

-4i+3 = 4-4i+i^{2} = (-i+2)^{2}

\sqrt{ (-i+2)^{2} } = -i+2

$z=x+iy$ form:

z=2-i

r=\sqrt{ \left( -1 \right)^{2}+\left( 2 \right)^{2} } = \sqrt{ 5 } \approx 2.2361

\phi = \arctan\left(-\frac{1}{2} \right) \approx-0.4636

$re^{i\phi}$ form:

\sqrt{ 5 } e^{-i\arctan(1/2)} \approx 2.2361e^{-i_{0}.4636}

c. $\sqrt{ 3-4i }$ Complete the square

-4i+3 = 4-4i+i^{2} = (-i+2)^{2}

\sqrt{ (-i+2)^{2} } = -i+2

$z=x+iy$ form:

z=2-i

r=\sqrt{ \left( -1 \right)^{2}+\left( 2 \right)^{2} } = \sqrt{ 5 } \approx 2.2361

\phi = \arctan\left(-\frac{1}{2} \right) \approx-0.4636

$re^{i\phi}$ form:

\sqrt{ 5 } e^{-i\arctan(1/2)} \approx 2.2361e^{-i_{0}.4636}

d. $e^{i\pi/4}$ $r=1, \ \phi=\frac{\pi}{4}$ $re^{i\phi}$ form:

e^{i\pi/4}

x = r\cos(\phi) = 1\cos \frac{\pi}{4} = \frac{1}{\sqrt{ 2 }} \approx 0.7071

y = r\sin(\phi) = 1\sin \frac{\pi}{4} = \frac{1}{\sqrt{ 2 }} = 0.7071

$z=x+iy$ form:

\frac{1}{\sqrt{ 2 }}+\frac{1}{\sqrt{ 2 }}i \approx 0.7071 + 0.7071i

6. Townsend 1.32 Townsend 1.32. Add the two complex numbers $z_{1} = 1$ and $z_{2} = e^{i\pi/3}$ by (a) adding the real and imaginary pieces together and (b) using geometry to "add the arrows" representing each of these complex numbers. Check that your results for the magnitude and phase of the complex number $z_{1}+z_{2}$ agree. Converting $z_{2}$ from $re^{i\phi}$ to $z=x+yi$ form

x = r\cos(\phi) = 1\cos\left( \frac{\pi}{3} \right) = \frac{1}{2}

y = r\sin(\phi) = 1\sin\left( \frac{\pi}{4} \right) = \frac{\sqrt{ 3 }}{2}

z_{2}=\frac{1}{2} + \frac{\sqrt{ 3 }}{2}i

Adding $z_{1}$ to this yields

z_{1+2} = \frac{3}{2} + \frac{\sqrt{ 3 }}{2}i

![[Pasted image 20240117111522.png]] 7. Townsend 1.38 Townsend 1.38. For a grating with $N$ equally spaced narrow slits, the amplitude for detecting a photon with a photomultiplier centered at point P in the detection plane is given by

z_{p} =re^{ikd_{1}}[1+e^{i\phi}+e^{i_{2}\phi}+e^{i_{3}\phi}+\dots+e^{i(N-1)\phi}]

Notice that each term in this series of terms can be obtained from the one preceding it by multiplying by $e^{i\phi}$. Thus, it is a geometric series that can be summed. (a). Show that the probability of detecting a photon is given by

z_{p}^{*}z_{p}=r^{2}\left( \frac{\left( \sin ^{2} \left( \frac{N\phi}{2} \right)\right)}{\sin ^{2}\left( \frac{\phi}{2} \right)} \right)

$$(b).Verifythatthisresultreducestothedouble-slitresult(1.60)forN=\mathrm{2.1.60}$$

z_{p}^{*}z_{p} = 4r^{2}\cos ^{2}\left( \frac{\phi}{2} \right)

$$a.Probabilityisgivenby$$

r^{2}(e^{ikd_{1}}\left[ \sum^{N}{1} e^{i(N-1)\phi} \right])^{*}(e^{ikd{1}}\left[ \sum^{N}_{1} e^{i(N-1)\phi} \right])

r^{2}e^{-ikd_{1}}e^{ikd_{1}} \left[ \sum^{N}{1} e^{-i(N-1)\phi} \right]\left[ \sum^{N}{1} e^{i(N-1)\phi} \right]

r^{2}\left[ \sum^{N}{1} e^{-i(N-1)\phi} \right]\left[ \sum^{N}{1} e^{i(N-1)\phi} \right]

S_{N} = 1\left( \frac{1-(e^{i\phi})^{N}}{1-e^{i\phi}} \right), \ S_{N}^{*}=1\left( \frac{1-(e^{-i\phi})^{N}}{1-e^{-i\phi}} \right)

r^{2}S_{N}^{*}S_{N} = r^{2}\left( \frac{1-(e^{i\phi})^{N}}{1-e^{i\phi}} \right)\left( \frac{1-(e^{-i\phi})^{N}}{1-e^{-i\phi}} \right)

r^{2}\left( \frac{(1-(e^{i\phi})^{N})(1-(e^{-i\phi})^{N})}{(1-(e^{i\phi}))(1-(e^{-i\phi})} \right) =

r^{2}\left( \frac{(1-(e^{iN\phi}))(1-(e^{-iN\phi}))}{(1-(e^{i\phi}))(1-(e^{-i\phi})} \right) =

r^{2} \frac{2-e^{iN\phi}-e^{-iN\phi}}{2-e^{i\phi}-e^{-i\phi}}

r^{2} \frac{1-\frac{e^{iN\phi}+e^{-iN\phi}}{2}}{1-\frac{e^{i\phi}+e^{-i\phi}}{2}}

\cos \phi= \frac{e^{i\phi}+e^{-i\phi}}{2} , \ \cos N\phi= \frac{e^{iN\phi}+e^{-iN\phi }}{2}

r^{2}\frac{1-\cos(N\phi)}{1-\cos(\phi)}

r^{2}\frac{2\left( 1-\cos\left( \frac{2N\phi}{2} \right) \right)}{2\left( 1-\cos\left( 2\frac{\phi}{2} \right) \right)}

r^{2}\frac{\frac{\left( 1-\cos\left( \frac{2N\phi}{2} \right) \right)}{2}}{\frac{\left( 1-\cos\left( 2\frac{\phi}{2} \right) \right)}{2}}

\sin ^{2} \frac{\phi}{2} = \frac{1-\cos{\left( \frac{2\phi}{2} \right)}}{2}, \ \sin ^{2} \frac{N\phi}{2} = \frac{1-\cos{\left( \frac{2N\phi}{2} \right)}}{2}

\text{Event probability = }r^{2}\left(\frac{ \sin ^{2}\left( \frac{N\phi}{2} \right)}{\sin ^{2}\left( \frac{\phi}{2} \right)} \right)

$$b.Fordoubleslitexperiment,N=2$$

z_{p}^{*}z_{p}=r^{2}\left( \frac{\left( \sin ^{2} \left( \frac{2\phi}{2} \right)\right)}{\sin ^{2}\left( \frac{\phi}{2} \right)} \right)

r^{2}\left( \frac{\left( \sin ^{2} (\phi)\right)}{\sin ^{2}\left( \frac{\phi}{2} \right)} \right)

\sin^{2} \phi =\frac{1}{2}(1-\cos(2\phi)),\ \sin^{2} \frac{\phi}{2} =\frac{1}{2}\left( 1-\cos\left( \frac{2\phi}{2} \right) \right) = \frac{1}{2}(1-\cos(\phi))

r^{2}\left( \frac{1-\cos(2\phi)}{1-\cos (\phi)} \right)

r^{2} \frac{2-2\cos ^{2}(\phi)}{1-\cos(\phi)}

r^{2}\frac{2(1 - \cos(\phi))(1 + \cos(\phi))}{(1-\cos (\phi))}

r^{2} 2(1+\cos (\phi))

r^{2}\left( \frac{4(1+\cos(\phi))}{2} \right)

r^{2} 4 \frac{1+\cos (\phi)}{2}

r^{2} 4\sqrt{ \frac{1+\cos \phi}{2} } ^{2}

r^{2} 4\cos ^{2}\left( \frac{\phi}{2} \right)

z_{p}^{*}z_{p} = 4r^{2}\cos ^{2}\left( \frac{\phi}{2} \right)

$$8.Whatisthespeedofheliumatomswithade-Brogliewavelengthof1.03angstroms?$$

\lambda=\frac{h}{mv}

1.03E-10 = \frac{6.626E-34}{(6.6464731E-27)v}

v= \frac{6.626E-34}{(6.6464731E-27)1.03E-10}

v \approx 967.8832 \frac{m}{s}