Functional Vector Space

Using the following equation,

$$\Psi (x,t)=\sum c_n{\psi }_n(x)$$

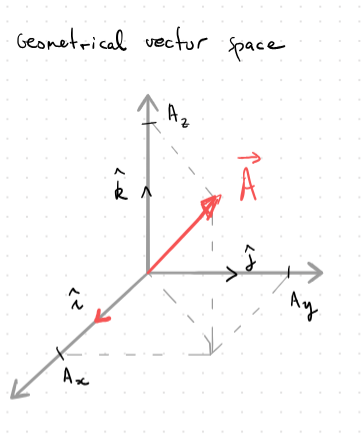
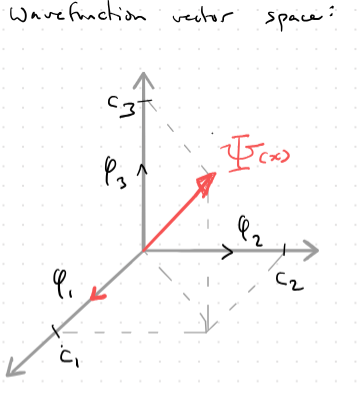
We can draw an analogy to geometrical vector space $\mathcal{V}$, where we have vectors $\vec{A},\vec{B}$ that are composed of unit vectors $\hat{i},\hat{j}\&\hat{k}$. If we take an analogy to wave-function vector space, we can compose objects (vectors), $\Psi (x,t)$ with unit vectors ${\phi }_n$ and ${\phi }_m^{\ast }$. ’ vs

Applying the above, we can have a basis vector:

$${\phi }_n(x)=\sqrt{\frac{2}{L}}\sin \left(\frac{n\pi x}{L}\right)$$

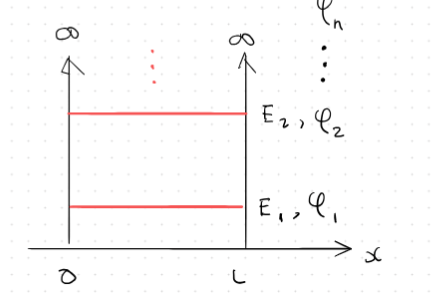
Represent an eigenfunction of the Hamiltonian operator $\hat{H}$ in the following equation:

$$\left[-\frac{{\hslash }^2}{2m}\frac{d^2}{d{x}^2}+V(x)\right]\phi (x)=E\phi (x)$$

where the Hamiltonian operator $\hat{H}$ is represented in the square brackets. If you solve for appropriate values of E and $\phi$, you can graph it:

$$\vec{A}=A_x\hat{i}+A_y\hat{j}+A_z\hat{k}$$