Problem 1
a) Explain the general principle of “electrical doping of graphene”.
Electrical doping of graphene alters the electrical properties of graphene, specifically shifting the Fermi energy away from the Dirac point. This is done by application of an electric field in a process called electrostatic grating.
b) Describe an experiment to measure the mobility of carriers in graphene. What values would you expect to be measured?
You could utilize the hall effect to measure the carrier mobility. To do this, you’d want to measure the intrinsic longitudinal resistivity. Then, apply a magnetic field to the graphene sample and measure the hall voltage produced. Using this, you could calculate the Hall coefficient, and then the carrier density. Then conductivity can be derived from the resistivity, and the carrier mobility can be calculated from conductivity and carrier density.
c) Compare the temperature dependence of the intrinsic carrier density in graphene and in a 3D semiconductor such as silicon. Which dependence do you think is best for device applications?
Graphene has a intrinsic carrier temperature dependence of approximately while silicon has values around
This demonstrates that graphene displays much less variation in intrinsic carrier density then silicon does, while scaling quadratically instead of exponentially. This would be a beneficial trait for some devices, especially those expected to work in high temperature environments.
d) Give an analytical expression for the optical absorption of graphene near a K point and calculate (in %) the absolute value of such absorption for a wavelength of 800 nm.
Absorption is independent of frequency in graphene, and is given by the following expression:
Where
The numerical value of this is given by
Where is the fine structure constant 1/137
e) Explain what is meant by “Pauli Blocking” in graphene.
Pauli Blocking refers to a string change in the interband absorption due to a shift in the Fermi energy. This effectively blocks transitions for photon energies of less then 2, while energies above are unaffected. This also allows for easy measurement of the Fermi energy.
f) Describe an experiment to measure the level of doping in graphene, also in relation to the phenomenon of Pauli blocking.
To determine the level of doping present within a graphene sample, one option would be to use photons of increasing energies and wait for a transition to occur. Using the Pauli blocking relation, this would allow the measurement of the Fermi energy level, which would allow you to determine the level of doping present.
g) Determine the number of layers in a graphene specimen displaying an optical absorp- tion of 10 %. Discuss your results and the prospects for using graphene multilayers as semitransparent electrodes.
Since graphene absorbs 2.29% of incident light, we can use the following relation
to determine that there is either 4 or 5 layers.
This tunable optical absorption has potential in areas such as optoelectronics, where transparent conductive materials are required. Graphene’s excellent electrical properties make it a promising candidate for this.
Problem 2
a) By using appropriate formulae and symbols, give a quantitative definition of the bulk (volume) polarization of a material.
The bulk polarization density for a dielectric homogeneous material is given by the following relation
Where chi is the electric susceptibility and epsilon naught is the electric constant.
b) Explain the difference between dielectric, paraelectric and ferroelectric (FE) materials, specifying in particular the relation of polarization vs. electric field for the different classes.
Dielectric materials encompass all materials that can be polarized by an applied electric field. This includes ferroelectrics and para-electrics. The distinguishing feature of para-electric materials is the nonlinear polarization curve, with a rapid polarization swap when the electric field is reversed. The distinguishing feature of Ferroelectric materials is the polarization hysteresis, with an electric field threshold needing to be reached in the opposite direction of polarization for the polarization to be swapped.
c) Draw a diagram of the polarisation (vs. electric field, E) for a ferroelectric material and explain the naming of this class of materials.
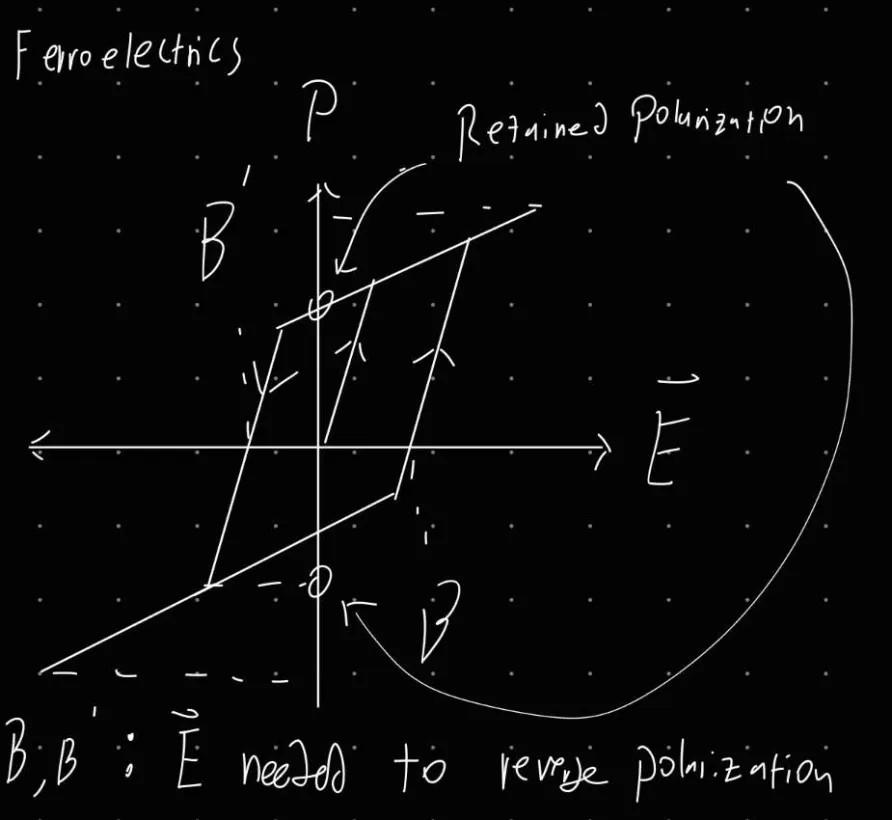 d) Explain why FE materials can be used to build electric memories.
Ferroelectric materials hysteresis’ properties can be used to maintain a state of polarization. This state memory can be used to create non-volatile memory that can switch very quickly. Additionally, the ferroelectric components can be built very small to facilitate dense memory arrays.
d) Explain why FE materials can be used to build electric memories.
Ferroelectric materials hysteresis’ properties can be used to maintain a state of polarization. This state memory can be used to create non-volatile memory that can switch very quickly. Additionally, the ferroelectric components can be built very small to facilitate dense memory arrays.
e) State what is the order parameter used in Landau’s theory to derive the phase transitions properties. The order parameter used in the Landau-devonshire thermodynamic description of ferroelectrics is the polarization of the material.
**f) State if the melting of an ice cube is a first order or a second order phase transition. **
The melting of an ice cube should be a fire order phase transition.
g) State what type are FE phase transitions. Ferroelectric phase transitions are second order transitions due to the continuous nature of the transition.
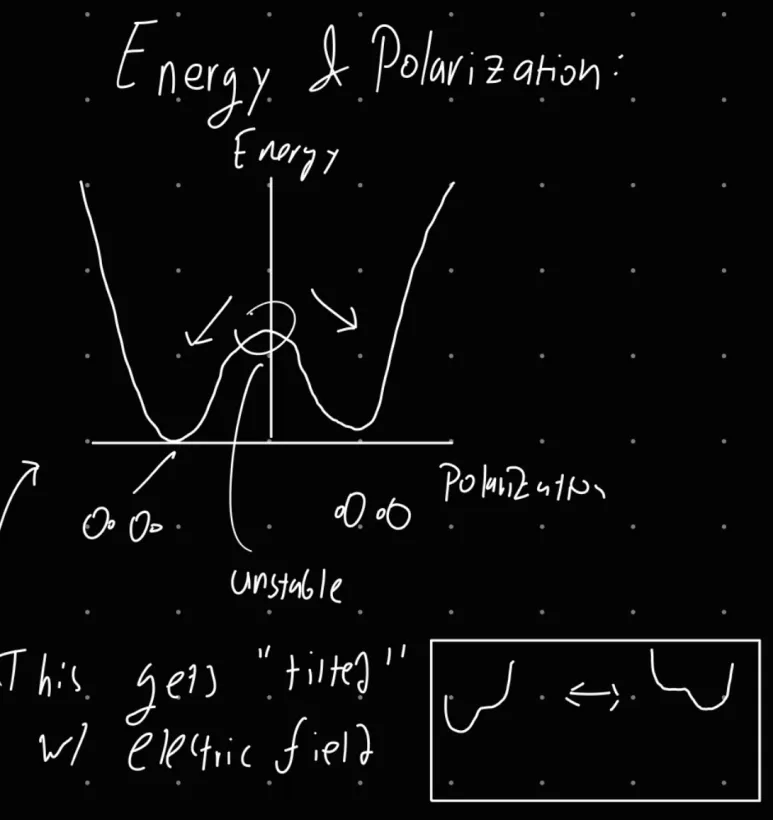
h) Explain the mechanism giving rise to hysteresis for a FE material, in terms of appropriate graphs of the free energy vs. the polarisation P in the significant points of the P vs. E characteristic.
The hysteresis in FE materials through the scope of free energy can be seen in the graph below. The two local minima represent the polarization states of the FE material, and this can be shifted with an application of electric field, as the smaller diagrams below show.
Problem 3
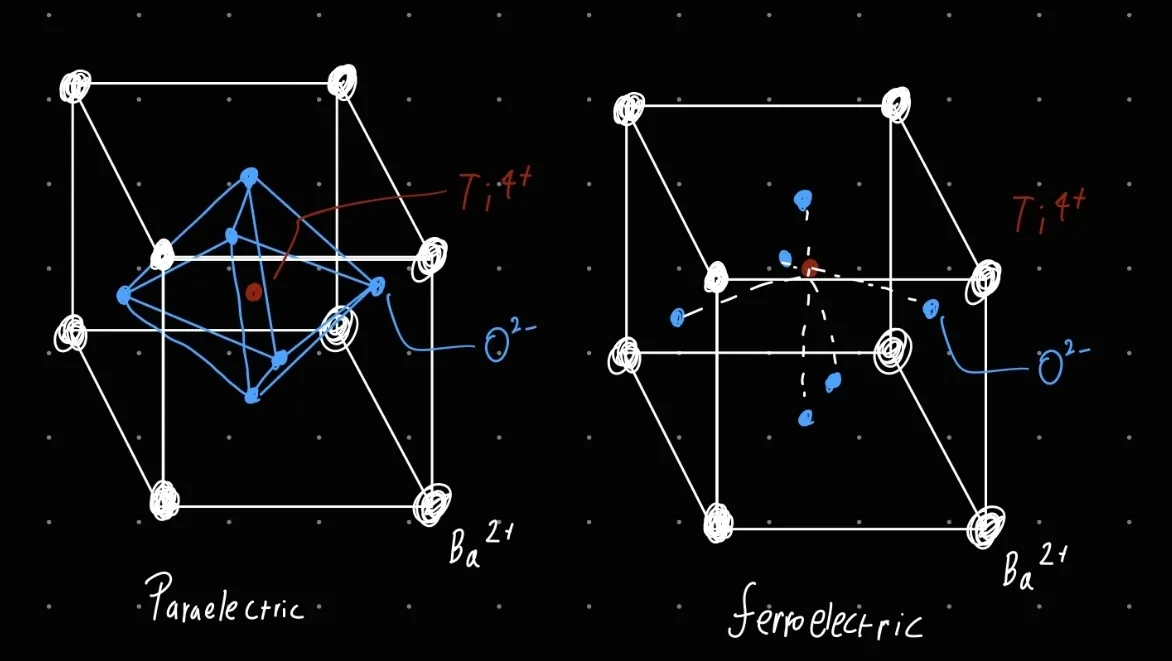
a) Draw the unit cell structure of the prototypical ferroelectric perovskite oxide barium titanate in its paraelectric and ferroelectric phase
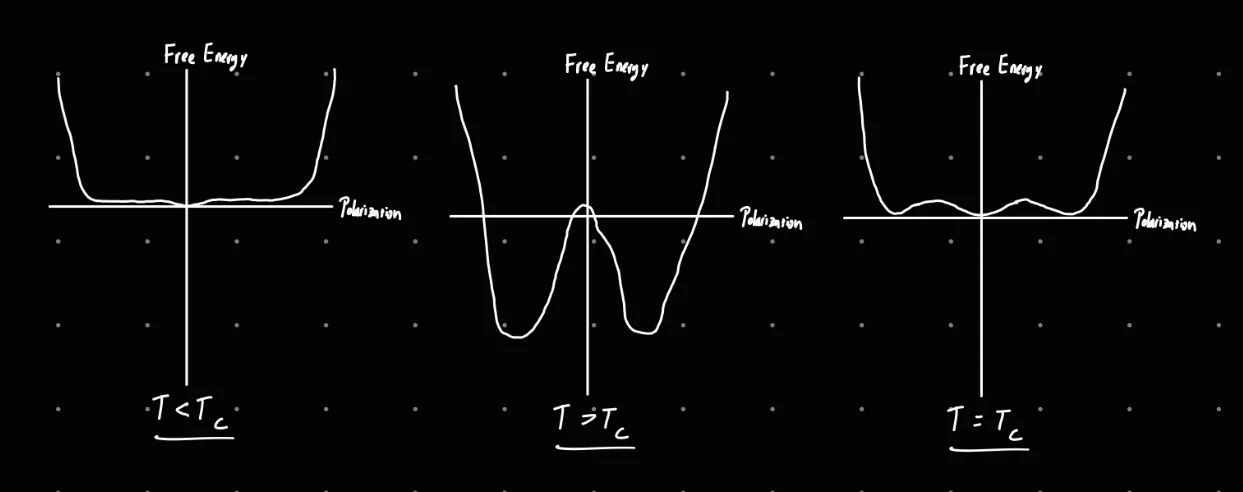
b) Draw a graph of the free energy as a function of polarisation at temperatures T = TC , T > TC and T < TC for a uniaxial FE crystal.
 c) Calculate the polarisation volume density arising as a result of the displacements indicated for the crystal, schematically indicated (as a two-dimensional projection) in the image below and undergoing a transition from cubic to tetragonal structure (represented on the left- and right-hand sides in the figure below, respectively). Hint: this can be considered a model for barium titanate - black filled circles represent Ba2+, white circles O2−, and the grey central circle Ti4+ ions.
c) Calculate the polarisation volume density arising as a result of the displacements indicated for the crystal, schematically indicated (as a two-dimensional projection) in the image below and undergoing a transition from cubic to tetragonal structure (represented on the left- and right-hand sides in the figure below, respectively). Hint: this can be considered a model for barium titanate - black filled circles represent Ba2+, white circles O2−, and the grey central circle Ti4+ ions.
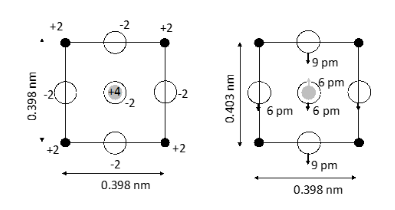 Polarization is given by dipole moment per unit volume
Polarization is given by dipole moment per unit volume
In the case of a cubic crystal structure the volume of the unit cell is given by
Which is cubic nanometers in this case.
This gives us the polarization if we take the displacement from the above figure of 6 picometers. We also know that the titanium ion is in the +4 oxidation state. is the elementary charge. This gives us the following expression:
r