Problem 9
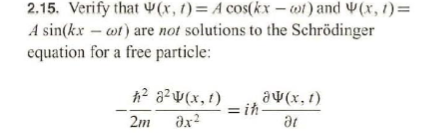
−2mℏ∂x2∂2(Acos(kx−ωt))=iℏ∂t∂(Acos(kx−ωt))
−2mℏ(−Ak2cos(kx−ωt))=iℏ(Aωsin(kx−ωt))
2mk2cos(kx−ωt)=iωsin(kx−ωt)
Therefore this is not a solution to the Schrodinger equation for a free particle
−2mℏ∂x2∂2(Asin(kx−ωt))=iℏ∂t∂(Asin(kx−ωt))
−2mℏ(−Ak2sin(kx−ωt))=iℏ(−Aωcos(kx−ωt))
2mk2sin(kx−ωt)=−iωcos(kx−ωt)
Therefore this is not a solution to the Schrodinger equation for a free particle
Problem 10

−2mℏ2∂x∂(c1ψ1+c2ψ2)=iℏ∂t∂(c1ψ1+c2ψ2)
−2mℏ2(∂x∂c1ψ1+∂x∂c2ψ2)=iℏ(∂t∂c1ψ1+∂t∂c2ψ2)
c1ψ1∝ψ1; c2ψ2∝ψ2
−2mℏ2∂x∂ψ1−2mℏ2∂x∂ψ2=iℏ∂t∂ψ1+iℏ∂t∂ψ2
−2mℏ2∂x∂ψ1=iℏ∂t∂ψ1
−2mℏ2∂x∂ψ2=iℏ∂t∂ψ2
∴−2mℏ2∂x∂ψ1+(−2mℏ2∂x∂ψ2)=iℏ∂t∂ψ1+iℏ∂t∂ψ2
Problem 11

((Ae−ikx+Beikx)(Aikeikx−Bike−ikx)−(Aeikx+Be−ikx)(−Aike−ikx+Bikeikx))
Expanded and simplified with wolfram
2ik(A2−B2)
jx=2miℏ(2ik(A2−B2))
jx=mℏk(A2−B2)
Problem 12

1=0∫LNx2(L−x)dx
N1=0∫Lx2(L−x)dx
Computed with wolfram
N1=12L4
N=L412
Finding expectation value for x
⟨x⟩=∫ψ∗xψdx
0∫L(L412x2(L−x))2xdx
L4120∫L(x2(L−x2))2xdx
Computed with wolfram
L412(60L8⋅(6L2−15L+10))
⟨x⟩=5L4⋅(6L2−15L+10)
Problem 13

⟨px⟩=−∞∫∞Ψ∗iℏ∂x∂(Ψ)dx
−∞∫∞e−ikxψ∗(x)iℏikeikxψ(x)dx
−∞∫∞e−ikxψ(x)iℏikeikxψ(x)dx
ℏk−∞∫∞ψ2(x)dx
−∞∫∞ψ2(x)dx=1
⟨px⟩=ℏk
Problem 14
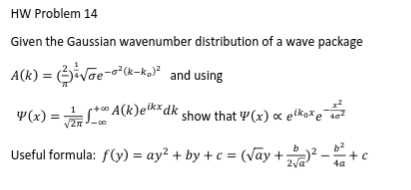
A(k)=(π2)1/4σe−σ2(k−k0)2
Ψ(x)=2π1−∞∫∞A(k)eikxdk
Ψ(x)=2π1−∞∫∞(π2)1/4σe−σ2(k−k0)2eikxdk
−∞∫∞e−a(k−k0)2xeikxdx
Multiply by
eik0xe−ik0x
You get
eik0x−∞∫∞e−a(k−k0)2eikxe−ik0xdk
eik0x−∞∫∞e−a(k−k0)2ei(k−k0)xdk
eik0x−∞∫∞e−ak′2eik′xdk′
eik0x−∞∫∞e−ak′2+ik′xdk′
(bk′+c)2=b2k′2+2cbk′+c2
b2k′2+2cbk′=(bk′+c)2−c2
ak′2+ik′x
b2=a
ak′2+ik′x=(ak′+2aix)−−4ax2
2bc=ix
c=2aix
rewrite int as
eik0x∫e−(ak′+(ix)/2a)2e−x2/4adx
eik0x∫e−u2e−x2/4adx
eik0xe−x2/4σ−∞∫∞e−u2du=π
u=−(ak′+(ix)/2a)2; du=2a(x−2ik)
We can drop the constants
∝eik0xe−x2/4σ
Ta-da
Problem 15
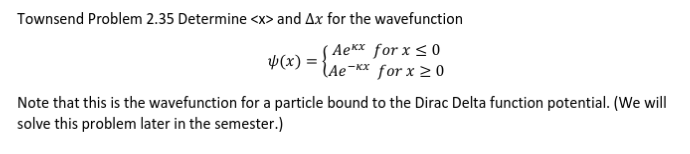 Normalize Wave functions
Normalize Wave functions
−∞∫∞ψ∗ψdx=1
1=−∞∫0A2e2κxdx+0∫∞A2e−2κxdx
A21=−∞∫0e2κxdx+0∫∞e−2κxdx
A21=2κ1+2κ1
A21=κ1
A2=κ∴A=κ
Finding ⟨x⟩
−∞∫0xκe2κxdx+0∫∞xκe−2κxdx
Integration by parts (wolfram)
−4κ1+4κ1
⟨x⟩=0
This corresponds to the graphical observation!
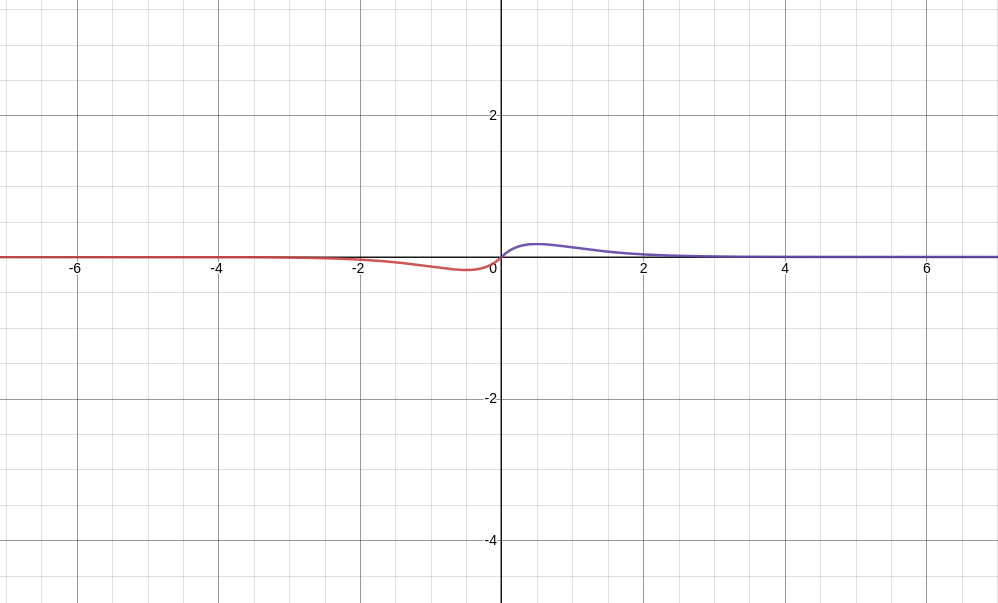
−∞∫0x2κe2κxdx+0∫∞x2κe−2κxdx
Use integration by parts (wolfram alpha)
4κ21+4κ21
4κ22=2κ21
2κ21
Δx=2κ21+02=0
Δx=κ121
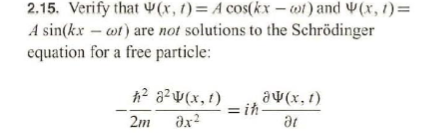




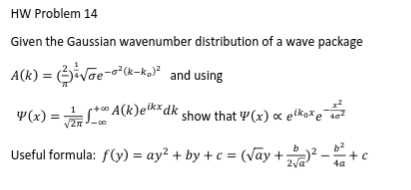
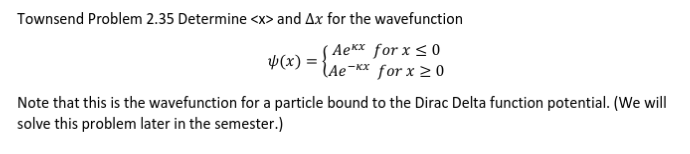 Normalize Wave functions
Normalize Wave functions