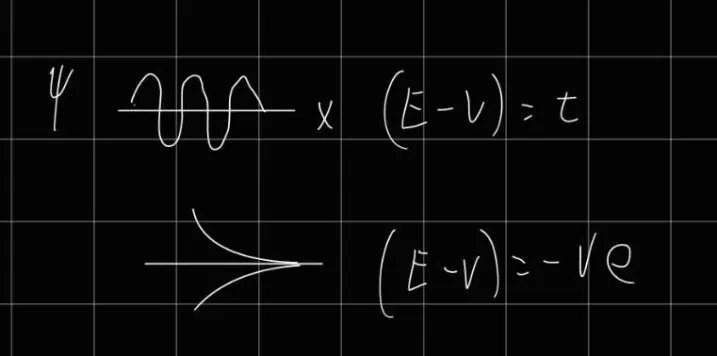Class 8 worksheet

1. Assume you know the energy eigenfunctions ${\Psi }_1(x,t)$ of the Hamiltonian operator and you find that $\int {\psi }^{\ast }(x){\Psi }_{2}d=0.1$ What is the probability of observing a particle energy of $\hslash {\omega }_2$ at any time?

$$\Psi (x)=\sum _i{c}_i{\psi }_i$$ $$C_i=\int \psi (x){\Psi }_i(x)dx$$ $$P(E_1)=C_1^{\ast }{C}_1=C_1^2$$ $$P(E_1)=0.01$$

2. A particle in a state given by $\Psi (x,t)=A({\psi }_1{e}^{(i{E}_{1}t/h)}+3{\psi }_2{e}^{i{E}_{2}t/\hslash })$ where $E_1=1eV$ and $E_2=5eV$ and both ${\psi }_1$ and ${\psi }_2$ are normalized a. What is the expectation value of a large number of energy measurements of this system? Explain.

$$A=\frac{1}{\sqrt{10}}\to C_1=\frac{1}{\sqrt{10}},C_3=\frac{3}{\sqrt{10}}$$ $$\frac{C_1^2{E}_1+C_2^2{E}_2}{2}$$ $$\frac{\frac{1}{10}(1eV)+\frac{9}{10}(5eV)}{2}$$ $$⟨E⟩=\frac{46}{10}\approx 4.6eV$$

The average of energy levels weighted by the constants of how “much” of each energy level there is yields the expectation value.

b. The most likely measurement is 5, because its a 90 percent chance

3. The spatial wavefunction of a particle decays monotonically to zero in a particular region of space. What can you say about the eigenenergy of the state relative to the potential energy in that region?

$$\frac{{\partial }^2\psi }{\partial x^2}\approx -(E-V)\psi$$