Paul Lea Homework 4

22. Townsend problem 3.5 The probability a measurement of $E$ yields $E_1$ is given by the following

$$|c_n{|}^2=P_n⟹\text{Prob. of }{E}_1=|\frac{i}{2}{|}^2\to \frac{1}{4}$$

The probability of yielding $E_1$ is $\frac{1}{4}$ We can use the similar method to find the probability of yielding $E_2$.

$$\text{Prob. of }{E}_2={\left(\frac{\sqrt{3}}{2}\right)}^2=\frac{3}{4}$$

We can double check that this accurate because the following condition has to hold true:

$$\sum _{n=1}^{\infty }|c_n{|}^2=1$$

and the sum of $\frac{1}{4}$ and $\frac{3}{4}$ does equal 1.

Finding the expectation value is relatively simple, by taking the weighted average of $E_n$ with the respective coefficients as follows:

$$⟨E⟩=\sum _{n=1}^{\infty }{P}_n{E}_n=\frac{1}{4}{E}_1+\frac{3}{4}{E}_2$$

To find the uncertainty, we can first follow a similar procedure to find $⟨E^2⟩$

$$⟨E^2⟩=\sum _{n=1}^{\infty }{P}_n{E}_n^2=\frac{1}{4}{E}_1^2+\frac{3}{4}{E}_2^2$$

Putting these into the uncertainty equation:

$$\Delta E=(⟨E^2⟩-{⟨E⟩}^2{)}^{1/2}$$ $$=\left[\frac{1}{4}(E_1^2+3E_2^2)-\frac{1}{16}(E_1+E_2{)}^2\right]\to \left[\frac{1}{4}(E_1^2+3E_2^2)-\frac{1}{16}(E_1^2+E_2^2+2E_1{E}_2)\right]$$ $$\left[\frac{1}{4}{E}_1^2+\frac{3}{4}{E}_2^2-\left(\frac{1}{16}{E}_1^2+\frac{9}{16}{E}_2^2+\frac{3}{8}{E}_1{E}_2\right)\right]$$

Simplifies down to:

$$\frac{3}{16}(E_1-E_2{)}^2$$

Which is a logical answer, because the uncertainty when $E_1=E_2$ 23. Townsend problem 3.8 We can exploit the orthogonality of eigenfunctions to solve this:

$$c_n=\int \Psi (x){\psi }_n(x)dx$$

We are given the normalized wavefunction above, so we just need the generalized eigenfunction. This is for the bound state of the infinite square well, so we can use the following:

$${\psi }_n=\sqrt{\frac{2}{L}}\sin \frac{n\pi x}{L}$$

Now we get to put it all together and solve:

$$c_n=\underset{0}{\overset{L}{\int }}\sqrt{\frac{30}{L^5}}x(L-x)\sqrt{\frac{2}{L}}\sin \frac{n\pi x}{L}dx$$

Start by pulling the constants out of the integration

$$=\sqrt{\frac{2}{L}}\underset{0}{\overset{L}{\int }}\sin \left(\frac{n\pi x}{L}\right)\sqrt{\frac{30}{L^5}}x(L-x)dx$$ $$\frac{2\sqrt{15}}{L^3}\left[L\underset{0}{\overset{L}{\int }}L\sin \left(\frac{n\pi }{L}x\right)dx-\underset{0}{\overset{L}{\int }}{x}^2\sin \left(\frac{n\pi }{L}x\right)dx\right]$$ $$\frac{2\sqrt{15}}{L^3}\left[L{\left[\left({\frac{L}{n\pi }}^2\right)\sin \left(\frac{n\pi }{L}x\right)-\frac{Lx}{n\pi }\cos (\frac{n\pi }{L}x)\right]}_0^L\right]$$ $$-{\left[2{\left(\frac{L}{n\pi }\right)}^{2}x\sin \left(\frac{n\pi }{L}x\right)-\frac{{\left(\frac{n\pi x}{L}\right)}^2-2}{{\left(\frac{n\pi }{L}\right)}^3}\cos \left(\frac{n\pi }{L}x\right)\right]}_0^L$$ $$\frac{2\sqrt{15}}{L^3}\left[-\frac{L^3}{n\pi }\cos (n\pi )+L^3\frac{(n\pi {)}^2-2}{(n{\pi }^3)}\cos (n\pi )+\frac{L^3}{(n\pi {)}^3}\cos (0)\right]$$ $$c_n=\frac{4\sqrt{15}}{(n\pi {)}^3}[\cos (0)-\cos (n\pi )]$$ $$c_n=\frac{4\sqrt{15}}{(n\pi {)}^3}[1-(-1{)}^n]$$ $$c_n^2=\frac{240}{n^6{\pi }^6}[1-(-1{)}^n{]}^2$$

24. Townsend problem 3.12 a. Probability of finding the ground state in the new well is given by $c_1^2$ if $c_1$ is real

$$c_1=\underset{-\infty }{\overset{\infty }{\int }}{\psi }_1(x)\Psi (x)dx$$ $$c_1=\underset{0}{\overset{L}{\int }}\sqrt{\frac{2}{2L}}\sin \left(\frac{\pi x}{2L}\right)\sqrt{\frac{2}{L}}\sin \left(\frac{\pi x}{L}\right)dx$$ $$c_1=\frac{\sqrt{2}}{L}\underset{0}{\overset{L}{\int }}\sin \left(\frac{\pi x}{2L}\right)\sin \left(\frac{\pi x}{L}\right)dx$$ $$c_1=\frac{4\sqrt{2}}{3\pi }$$ $$c_1^2=\frac{32}{3\pi }$$

This is the probability of finding the system in the ground state. The probability of finding the system in the first excited state, $c_2$ can be found with a similar process.

$$c_2=\underset{0}{\overset{L}{\int }}\sqrt{\frac{2}{2L}}\sin \left(\frac{2\pi x}{2L}\right)\sqrt{\frac{2}{L}}\sin \left(\frac{\pi x}{L}\right)dx$$ $$c_2=\frac{\sqrt{2}}{L}\underset{0}{\overset{L}{\int }}\sin \left(\frac{\pi x}{L}\right)\sin \left(\frac{\pi x}{L}\right)dx$$ $$c_2=\frac{\sqrt{2}}{L}\frac{L}{2}$$ $$c_2^2=\frac{1}{2}$$

b. The time development of the system, we will use the following procedure:

$${\psi }_n(t)=\sqrt{\frac{1}{L}}\sin \left(\frac{n\pi x}{2L}\right)e^{i{E}_n^{\prime }t/\hslash }$$

The system is in a stationary state. 25 Townsend 4.04 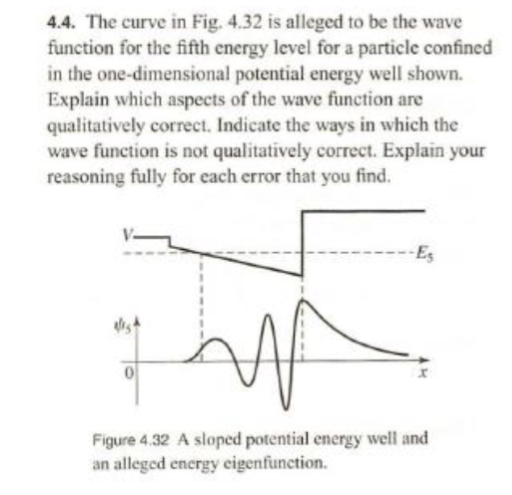Correct:

1. The figure shows the eigenfunction decaying to 0 at both ends, which makes sense because the potential is greater then the energy level.
2. The figure shows the frequency of oscillation increasing when the potential decreases, corresponding to higher energy levels and lower wavelength in that region.
3. The figure shows the correct overall waveform for the 5th energy level.

Incorrect:

1. Wave-function should have higher amplitude on the left side of the sloped potential.