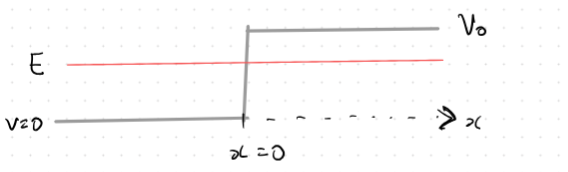
Solutions for E from:
What happens if ? (energy is greater then potential)
 We can take the Time independent Schrodinger equation
We can take the Time independent Schrodinger equation
Where
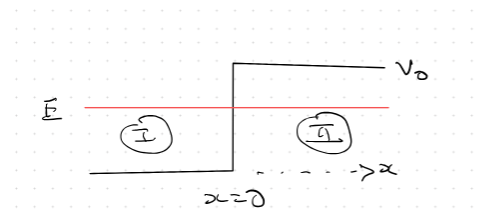 Now Consider Regions 1 and 2
Region 1: For ;
Now Consider Regions 1 and 2
Region 1: For ;
Solutions:
Region 2: For ,
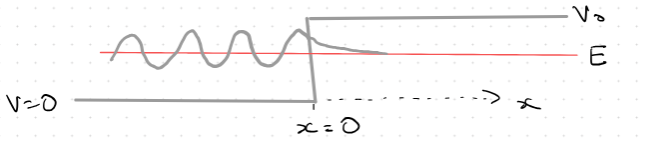
What happens if E > V everywhere?
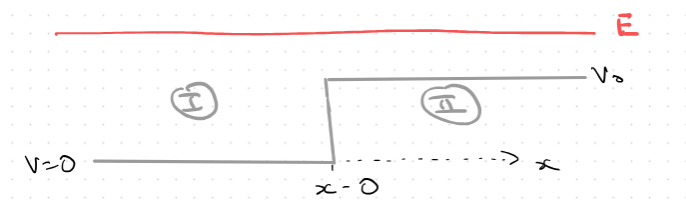 Region I:
with solution:
Region I:
with solution:
Region II:
with solution:
Consider incident traveling wave from the left:
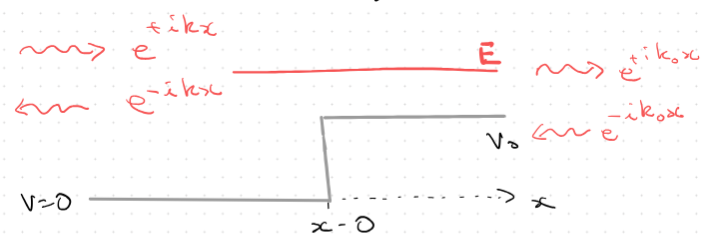 In the above diagram:
In the above diagram:
Region 1
Represents flux coming from the left and Represents the flux reflected from the potential
for and for
**no wave incident from
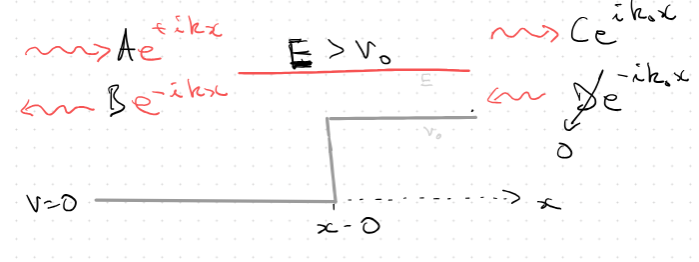
There is reflection and transmission: Lets use the probability current to quantify this: Recall:
Now, $$ R\equiv\frac{j_{ref}}{j_{inc}} ; T \equiv \frac{j_{trans}}{j_{inc}}
\phi_{(x,t)} = \int A(k)e^{i(kx-\omega t)} , dx