2023-12-05 Quantum Physics Lecture

Exam 3

• Do course evaluation
• Review for class 26
• AEFIS Course evaluation (10 bonus) points
• Exam #3 on Friday
  • Half on exam 1+2 and half on after that
• More questions then less challenging per question
• Can keep same partners or switch
• Redo exam 1 and 2, and in-class assignments

Review

Quantum Physics- Language of life at the nanoscale

Math Background

• Complex #‘s, Eulers formula;

$$z=r{e}^{i\theta },i=\sqrt{-1}$$

• Solving PDE’s
  • Ansatz
  • Boundry Condititions
  • Seperation of variables

Light as a wave

• Solution to wave problem with ansatz
• Interference problems

$$E(d,0)=e^{ik{d}_1}(1+e^{ik\Delta d})$$

• Double slit problem
  • Constructive Interference
  • Maxima and Minima

$$d\sin (\theta )=n\lambda$$

• Single Slit problem
  • Large central maxima (~20x surrounding)

$$a\sin (\theta )=m\lambda$$

• M is for minima, N is for maxima

X-Ray diffraction from crystals

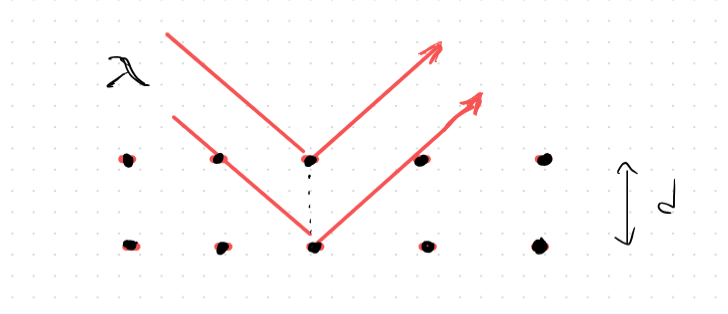
• Using diffraction and interference to find lattice constant of materials

$$\sin (\theta )=\frac{n\lambda }{2d}$$

• $d$ is lattice constant

Photoelectric experiment

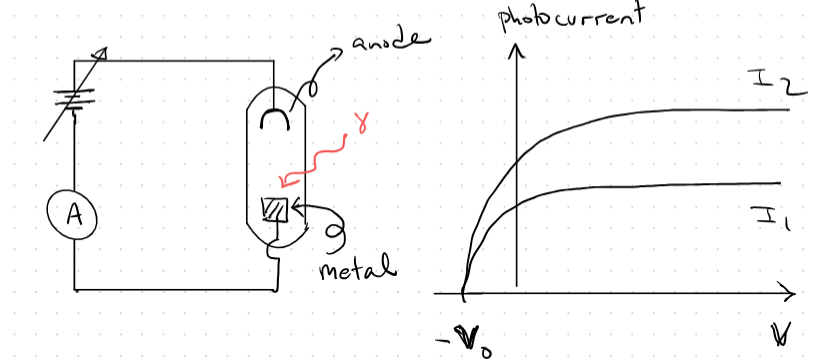
• Evidence that light is made of photons
• Increasing intensity does not increase current

$$h\nu =w+k$$

• Where $w\equiv$ work function of material (constant based on material
• Max energy on left, kinetic energy + work constant on right

Wave nature of matter

• De Broglie wavelength:

$$\lambda =\frac{h}{p}$$

• Interference of matter
• Rough estimate of uncertainty principle

$$\Delta y\Delta p\sim h$$

Schrodinger equation

• Clever guess by Schrodinger

$$-\frac{{\hslash }^2}{2m}\frac{d^2\psi (x,t)}{d{x}^2}+V(x)\psi (x,t)=i\hslash \frac{d\psi (x)(x,t)}{dt}$$

• First term is kinetic energy , second is potential, right hand is total
• Hamiltonian is right hand side
• Momentum Operator is given by

$$\frac{\hslash }{i}\frac{d\psi }{dx}$$

• Typical guess for particle in free space (no potential)

$$\psi (x,t)=e^{i(kx-\omega t)}$$

• Normalization

$$\int |{\psi }^{\ast }\psi |dx=1$$

• Classically you can track the position of things, quantum mechanically $\psi (x,t)$ yields the probability that is at a given location
• If you have an uncertainty of position you cant follow the trajectory
• Psi encodes the information about the object
• Probability Density is

$$|\psi (x,t){|}^2$$

• Depicts how probability changes over space. Can be used to find most probable location for particle.
• Probability Density times infinitesimal distance is probability

$$\left[\frac{|\psi (x,t){|}^2}{dist}\right]\cdot \Delta x=prob$$

• Integrating free space guess over all space

$$\psi (x,t)=e^{i(kx-\omega t)};\int \psi (x,t)dx=0orDNE$$

• Integrating 1 over all space is infinity, using a wave packet prevents this
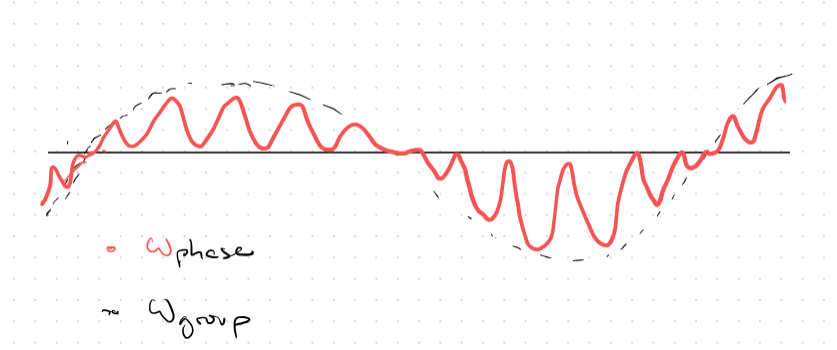
• Group vs Phase velocity
• Wave function
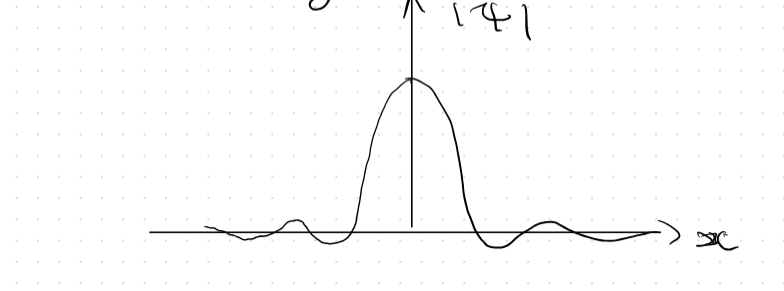
• Gaussian-Like distribution
• Oscillations at edges are wrong for Gaussian

Quantum Mech. Basics

• Expectation value is given by

$$<x>=\sum _{i}pro{b}_i{x}_i=\int {\psi }^{\star }x\psi dx$$

• “Real” Heisenberg Uncertainty Principle

$$\Delta x\Delta p\ge \frac{\hslash }{2}$$

• Uncertainty is given by

$$\Delta A^2=<A^2>-<A{>}^2$$

Time independent S.E

$$-\frac{{\hslash }^2}{2m}\frac{d^2\psi (x)}{d{x}^2}+V(x)\psi (x)=E\psi (x)$$

• Using separation of variables see Time independent Schrodinger equation
• See also -time evolution

$$\psi (x,t)=\psi (x)e^{iEt/\hslash }$$

Functional Vector Space

$$\vec{A}=A_x\hat{i}+A_y\hat{j}+A_z\hat{k}$$

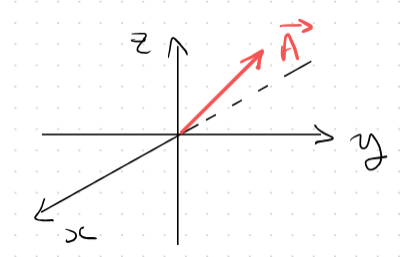
Energy Eigenvalue Problem

Gives you energy for an eigenvector

Bound state problems

• 3 main types
  • Infinite Square well
  • Harmonic Oscillator
  • Finite Square well
• Solutions for each
  • Infinite Square well

$${\phi }_n\sim \sqrt{\frac{2}{L}}\sin \left(\frac{n\pi x}{L}\right)$$ $$E_n=\frac{n^2{\pi }^2{\hslash }^2}{2m{L}^2}$$

Scattering from step potentials

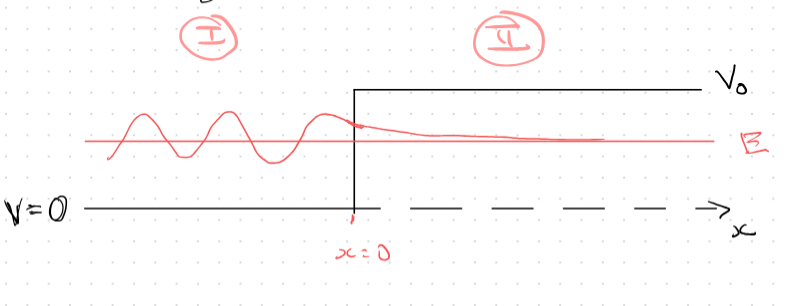
• Above is example with no reflection, quantum transmission (not tunneling) 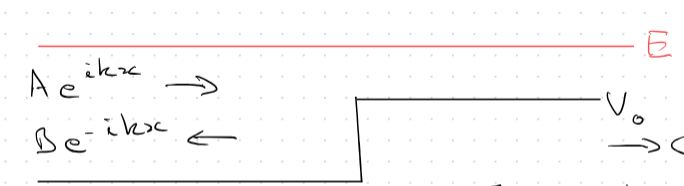Example with potential less then energy
• There is A, B, and C but no D because no energy is reflected off the infinite right side

Quantum Tunneling

Principles of QM

• Hermitian Operators
  • Operators linked to observables
  • Eigenfunctions orthogonal
  • Form complete set

$$\int {\phi }^{\star }(A\phi )dx=\int (A\phi {)}^{\star }\phi dx$$

• Matrix representation

$$<A>=\int {\psi }^{\star }\hat{A}\psi dx=\left(\begin{array}{cccc}{c}_1^{\star }& c_2^{\star }& \dots & \end{array}\right)\left(\begin{array}{cc}{A}_{11}& A_{12},\dots \\ & \\ A_{21}& \dots \\ & \\ \dots & \dots \end{array}\right)\left(\begin{array}{c}{c}_1\\ c_2\\ c_3\\ \dots \end{array}\right)$$

• No DiffEq representation of spin
• Spin emerges from Dirac equation (reviewed in IQM)
• Commutation Relations

3D Problems

• Cartesian vs Spherical cords
• Examples used are 3D box, H-atom
• Angular momentum

$$\vec{L}=\vec{r}\times \hat{p}$$

Angular momentum on z axis

$${\hat{L}}_z=\frac{\hslash }{i}\frac{d}{d\varphi }\to {\hat{L}}_z\Phi =m\hslash \Phi$$

$\hat{L}_{z}$ and $\hat{L}_{y}$ commute, but $\hat{L}_{x}$ and $\hat{L}_{y}$ do not

Hydrogen-Like atom

$$\psi (r,\theta ,\varphi )=R(r)Y_{lm}(\theta ,\varphi )$$

• Any particle with 1 electron is hydrogen-like. Neutrons and Protons don’t really matter. Multi particle systems not covered until grad level. Potential for HLS given by

$$V(r)=-\frac{z{e}^2}{4\pi {ϵ}_{0}r};z=1$$

Solution for R?

$$R(r)=r^{l}Fn(r)e^{-\sqrt{2m_{0}E/{\hslash }^2}r}$$

Energy levels given by:

$$E_n=-\frac{(13.6ev)Z^2}{n^2};n=1,2,3,\dots$$

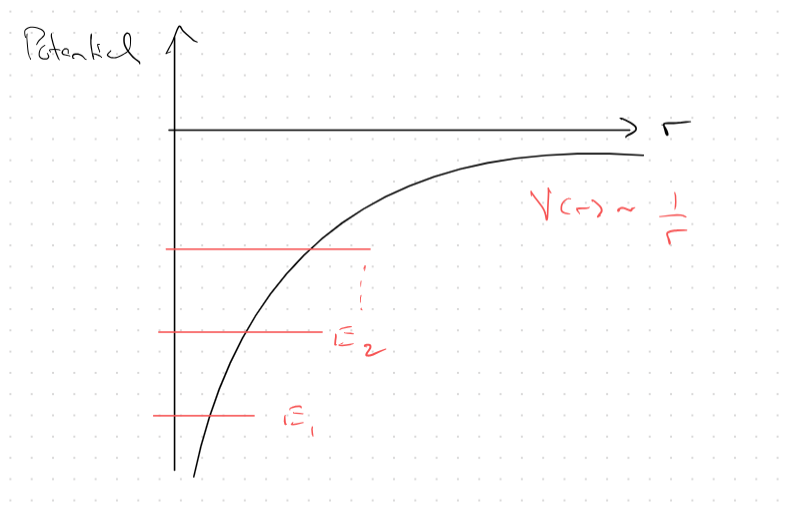
Coulomb Potential shown above. Bound state. N is quantum number for $L_z$ Particle is in bound state because E is less then V. See also 1 dimensional bound state.

Zeeman Effect

• Splitting of spectral lines due to magnetic field

$$u=-\vec{\mu }\cdot \vec{B}=\hat{H}$$ $$\vec{\mu }=\frac{q}{2m_0}\hat{L}$$

Intrinsic spin

• Stern-Gerlach Experiment
• g-factor (fudge factor)

$$\vec{\mu }=g\frac{\mu B}{\hslash }\vec{s}$$ $$|\vec{s}|=\sqrt{\frac{1}{2}\left(\frac{1}{2}+l\right)}\hslash$$ $$s=\frac{1}{2}$$ $$\Psi (x,t)\to \Psi (x,t)\chi (t)$$ $${\hat{H}}^{\prime \prime }=-{\vec{\mu }}_s\cdot \vec{B}$$

${\hat{H}}^{\prime \prime }$ is the spin derivative of the hamiltonian

$$\hat{H}=H_0+H^{\prime }+H^{\prime \prime }$$

Qubits (Bloch Sphere)

The chi vector is a state in a Qubit Qubit is system of spin vectors? IBM Quantum Computer uses superconducting qubits