3D problems
Review from 2023-10-31 Quantum Physics Lecture 18- - Commutation Relations - Eigenvalue and Eigenfunctions - Quantum Postulates - Properties of Hermitian Operators - Matrix Representations of Hermitian Operators
Bound States and Free particle
- Similar to 2-d problems, there are “free” states and “bound”’ states.

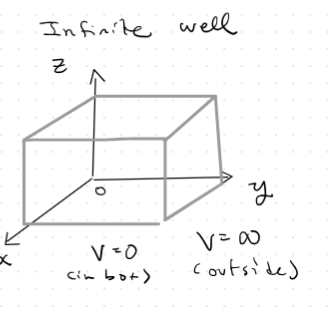
- We can use separation of variables in Cartesian/spherical coordinate systems.
- Potential can be modeled by the following: $$ V(r) \propto -\frac{1}{r} \propto \frac{1}{\sqrt{ x^{2}+y^{2}+z^{2} }}
-\frac{\hbar^{2}}{2m} \left[ \frac{d^{2}\psi}{dx^{2}}+\frac{d^{2}\psi}{dy^{2}} +\frac{d^{2}\psi}{dz^{2}} \right]= E\psi(x,y,z)
\Psi(x,y,z) = \phi_{x}(x) \phi_{y}(y)\phi_{z}(z)
![[Pasted image 20231114110540.png]] ### Three Dimensional [[Notes/Physics/Quantum Physics/Concepts/Time independent Schrodinger equation]]-\frac{\hbar^{2}}{2m} \left[ \frac{d^{2}\psi}{dx^{2}}+\frac{d^{2}\psi}{dy^{2}} +\frac{d^{2}\psi}{dz^{2}} \right]= (E-V(r))\psi(x,y,z)
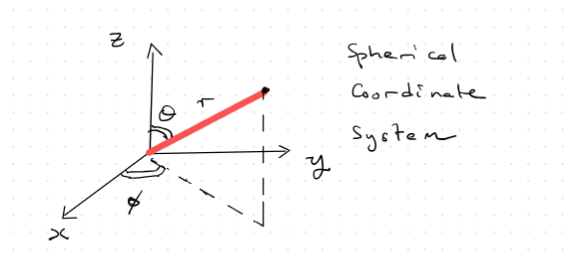
NB- This can also be represented with the Laplacian operator $\nabla^{2}$. ### Spherical Coordinate Overview $x = r\sin \theta \cos \phi$ $y=r\sin \theta \sin \phi$ $z=r\cos \theta$ Where the $\phi$ is known as the *azimuthal* angle, $\theta$ is the *polar* angle and $r$ is the radius. These two angles are shown below: ![[Pasted image 20231114200719.png]] The Laplacian in spherical coordinates is given below: $$ -\frac{\hbar^{2}}{2m} \left[ \frac{1}{r^{2}} \frac{d}{dr}\left( r^{2} \frac{d}{dr} \right) + \frac{1}{r^{2}\sin \theta} \frac{d}{d\theta} \left( \sin \theta \frac{ d}{d\theta} \right) + \frac{1}{r^{2} \sin ^{2}\theta} \frac{d^{2}}{d\phi^{2}} \right] \psi(r,\theta,\phi) = (E-V(r)) \psi(r,\theta,\phi) $$ This gives rise to the momentum operator in three dimensions: $\mathbf{P}$, as well as the more interesting angular momentum operator $\mathbf{L}_{op}$, which will be covered more in next class.\mathbf{P}^{2} = -\hbar^{2} \nabla^{2}
\mathbf{L} = -\hbar^{2}\left[ \frac{1}{\sin \theta} \frac{d}{d\theta} \left( \sin \theta \frac{d}{d\theta} \right) + \frac{1}{\sin \theta} \frac{d^{2}}{d\phi^{2}} \right] = \mathbf{r} \times \mathbf{p}
The rotational kinetic energy term in the Hamiltonian (RHS of following) is also equal to the angular momentum over $2mr^{2}$\frac{\mathbf{L}^{2}_{op}}{2mr^{2}} = -\frac{\hbar^{2}}{2m}\left[ \frac{1}{r^{2}\sin \theta} \frac{d}{d\theta} \left( \sin \theta \frac{ d}{d\theta} \right) + \frac{1}{r^{2} \sin ^{2}\theta} \frac{d^{2}}{d\phi^{2}} \right]
### Separation of Variables in Spherical Coordinates Replacing the Hamiltonian operator with $\left( \frac{\hat{P}_{r}^{2}}{2m} + \frac{\hat{L}^{2}}{2mr^{2}} \right)$, we get $$ \left( \frac{\hat{P}_{r}^{2}}{2m} + \frac{\hat{L}^{2}}{2mr^{2}} \right) \Psi(r,\theta,\phi)=(E-V(r))\Psi(r,\theta,\phi)Replacing with